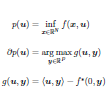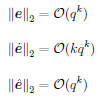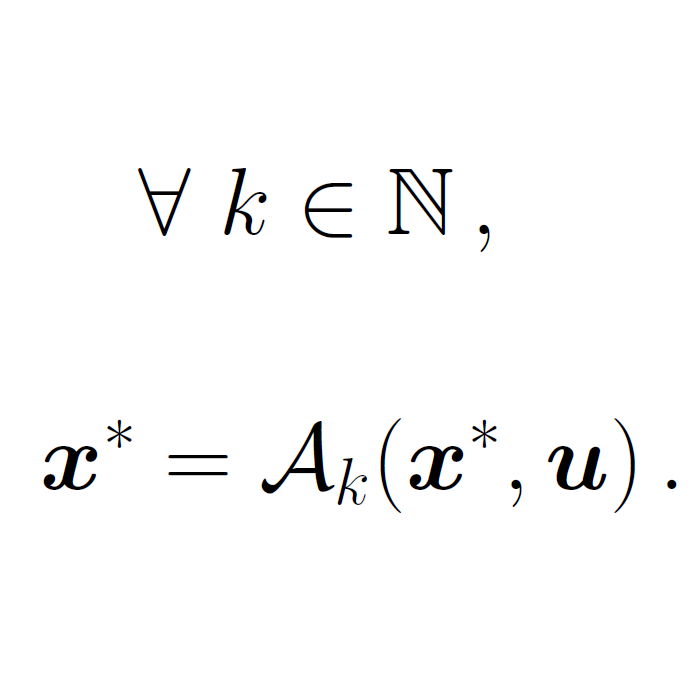Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Bilevel Optimization and Automatic Differentiation

The bilevel optimization problems that we consider are constrained minimization problems (upper level), where the constraint set is given as the set of solutions to another optimization problem (lower level), which depends on the upper level's optimization variable. In the context of computer vision or machine learning, bilevel optimization problems can be seen as a formalization of a parameter learning problem. The optimization variable is a parameter (vector) and the objective of the upper level is a loss function, which seeks to minimize the discrepancy between the solution of an energy minimization problem and some ground truth data for a given parameter.
In general, bilevel optimization problems are hard to solve, and this is particularly true in the context of machine learning and computer vision. The reason for this is that, on the one hand, the data is usually high-dimensional (often also the parameter vector is high-dimensional) and, on the other hand, the energy minimization problems in the lower level are often naturally non-smooth. In this research project, we aim to solve and understand such bilevel optimization problems.
Moreover, a successful approximation strategy is the substitution of the lower level problem by an iterative (unrolled) algorithm for solving this problem. Using gradient based optimization for the overall bilevel problem comes down to efficiently computing the sensitivity of the solution mapping or, in the case of unrolled algorithms, the derivative of the unrolled iterative process. This process is known as Automatic Differentiation or, in Machine Learning context, Backpropagation. Key challenges are the memory efficiency of automatic differentiation and the convergence of the derivative sequence to the true derivative of the solution mapping of the lower level problem.

Partially funded by the German Research Foundation (DFG Grant OC 150/4-1).

Our Contribution:

	P. Ochs, R. Ranftl, T. Brox, T. Pock: Bilevel Optimization with Nonsmooth Lower Level Problems. In J.-F. Aujol, M. Nikolova, N. Papadakis (Eds.): International Conference on Scale Space and Variational Methods in Computer Vision (SSVM). Lecture Notes in Computer Science, Vol. 9087, 654-665, Springer, 2015. (Best Paper Award)
	P. Ochs, R. Ranftl, T. Brox, T. Pock: Techniques for gradient based bilevel optimization with nonsmooth lower level problems. Journal of Mathematical Imaging and Vision, 56(2):175-194, 2016. (Invited Paper)

The complexity of such bilevel optimization problems restricts us to local optimization methods. Moreover, the high dimensionality prohibits the usage of higher order information, and we have to apply first-order optimization schemes. However, gradient-based algorithms require a certain degree of smoothness of the objective function, which heavily relies on the smoothness of the lower level's solution mapping. We developed a strategy to approximate the lower level with a smooth iterative algorithm, which represents the non-smooth lower level problem exactly in the limit. Using this strategy, we solve a problem that is closer to the original problem than previous approaches.

S. Mehmood, P. Ochs:
Differentiating the Value Function by using Convex Duality.

International Conference on Artificial Intelligence and Statistics, 2021.

On the trace of non-smooth structures for which classic derivatives can be estimated, the value function is investigated, which appears in applications in Machine Learning such as structured support vector machines, matrix factorization and min-min or minimax problems in general. The objective of a parameteric optimization problem can be differentiated efficiently using convex duality. Connecting this idea with the dual optimization problem leads to efficient algorithms and convergence rates for computing these derivatives.

S. Mehmood, P. Ochs:
Automatic Differentiation of Some First-Order Methods in Parametric Optimization.

International Conference on Artificial Intelligence and Statistics, 2020.

Since the convergence of the derivative through the iteration maps of an algorithm is not very well understood, we revisit the convergence of derivatives obtained by Automatic Differentiation for smooth optimization algorithms. In particular, we show that the accelerated rate of convergence of the Heavy-ball method for smooth strongly convex optimization problems is reflected in an accelerated rate of convergence for the sequence of derivatives computed by AD of through the algorithm's update steps.

S. Mehmood, P. Ochs:
Fixed-Point Automatic Differentiation of Forward--Backward Splitting Algorithms for Partly Smooth Functions.

Technical Report, ArXiv e-prints, arXiv:2208.03107, 2022.

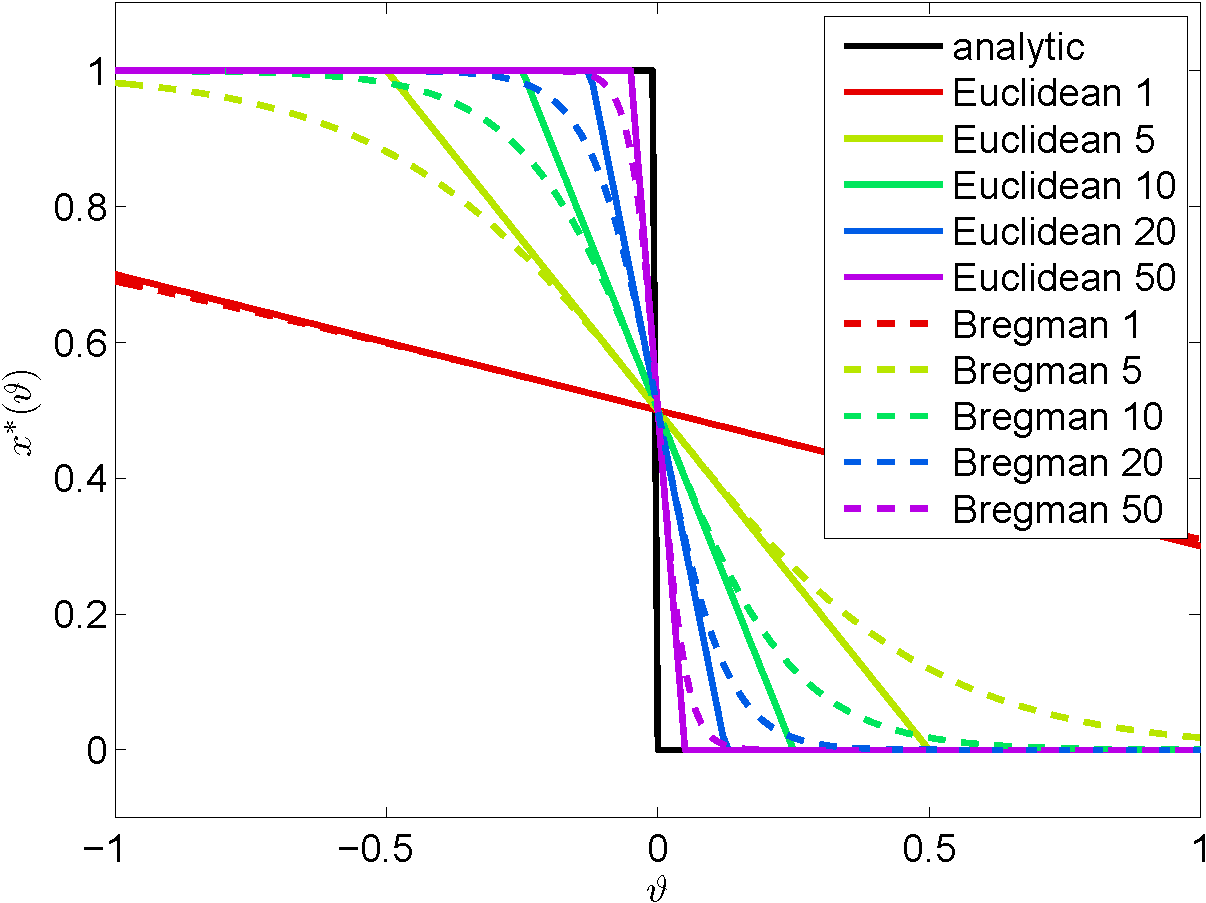
Going one step further, we analyze the derivative sequence for non-smooth lower level problems with the additional property of partial smoothness [Lewis02] A.S. Lewis: Active sets, nonsmoothness, and sensitivity. SIAM Journal on Optimization 13(3):702-725, 2002. . This favorable property is widely present in problems in machine learning and computer vision and has already led to deep insights of the behavior of first-order algortihms. Key is an identification result that states that the solution lies on a manifold and the algorithm identifies this manifold after a finite number of iterations and converges to the solution along the manifold (usually with a linear rate of convergence) [LFP17] J. Liang, J. Fadili, and G. Peyre: Activity identification and local linear convergence of forward-backward-type methods. SIAM Journal on Optimization 27(1):408-437, 2017. . For limit points that satisfy a certain non-degeneracy assumption, we prove convergence, including a linear convergence rate, for the sequence of derivatives that is generated along accelerated proximal gradient descent.

S. Mehmood, P. Ochs:
Automatic Differentiation of Optimization Algorithms with Time-Varying Updates.

Technical Report, ArXiv e-prints, arXiv:2410.15923, 2024.

Numerous Optimization Algorithms have a time-varying update rule thanks to, for instance, a changing step size, momentum parameter or, Hessian approximation. In this paper, we apply unrolled or automatic differentiation to a time-varying iterative process and provide convergence (rate) guarantees for the resulting derivative iterates. We adapt these convergence results and apply them to proximal gradient descent with variable step size and FISTA when solving partly smooth problems. We confirm our findings numerically by solving l1 and l2-regularized linear and logisitc regression respectively. Our theoretical and numerical results show that the convergence rate of the algorithm is reflected in its derivative iterates.