Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Inertial Algorithms for Non-smooth Non-convex Optimization

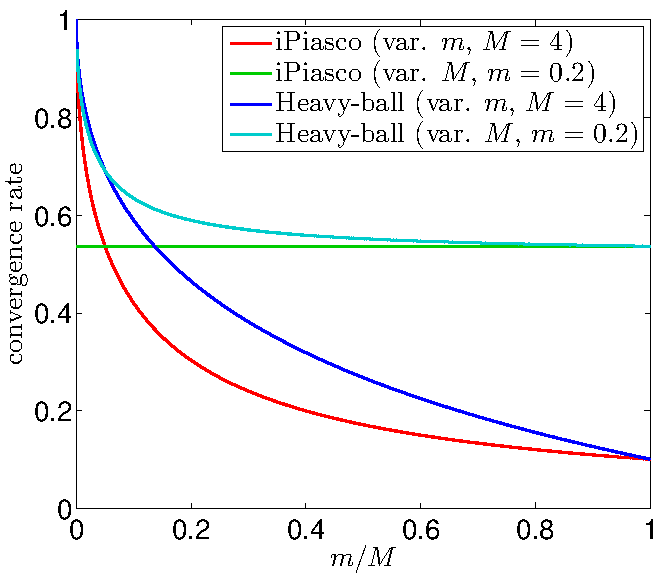
The inertial algorithms that we study are motivated from physics, namely from a dynamical system that describes the behaviour of a ball that is rolling down a surface subject to friction (also known as heavy-ball dynamical system). The motion of the ball accelerates due to inertia. In analogy to that, the considered algorithms generate a sequence of points that accelerates when it moves in the same direction as before. A classic method for smooth unconstrained optimization problems is the Heavy-ball method. It was introduced by Polyak in 1964 in a paper with the title "Some methods of speeding up the convergence of iteration methods" [Polyak64] B.T. Polyak: Some methods of speeding up the convergence of iteration methods. USSR Computational Mathematics and Mathematical Physics 4(5):1--17, 1964. , which suggests an improved performance of inertial algorithms. The global convergence of the Heavy-ball method for non-convex problems was studied by Zavriev and Kostyuk [ZK93] S.K. Zavriev and F.V. Kostyuk: Heavy-ball method in nonconvex optimization problems. Computational Mathematics and Modeling 4(4):336--341, 1993. . For the mechanical interpretation, we refer to [AGR00] H. Attouch, X. Goudou, and P. Redont: The heavy ball with friction method, i. the continuous dynamical system: global exploration of the local minima of a real-valued function by asymptotic analysis of a dissipative dynamical system. Communications in Contemporary Mathematics 2(1):1--34, 2000. .

In convex optimization the Heavy-ball method and its variations have led to the study of so-called accelerated schemes and optimal methods [Nesterov04] Y. Nesterov: Introductory lectures on convex optimization: A basic course. Applied Optimization, vol. 87, Kluwer Academic Publishers, 2004. , which refers to algorithms with a theoretical worst-case complexity that is of the same order as the lower complexity bound for a certain class of problems. This topic is still actively researched.

Our Contribution:

P. Ochs, Y. Chen, T. Brox, T. Pock:
iPiano: Inertial Proximal Algorithm for Non-convex Optimization.

SIAM Journal on Imaging Sciences, 7(2):1388-1419, 2014.

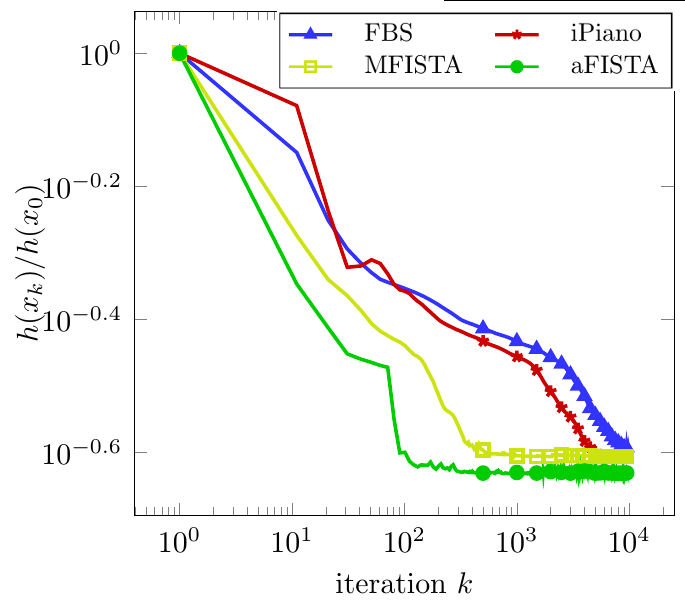
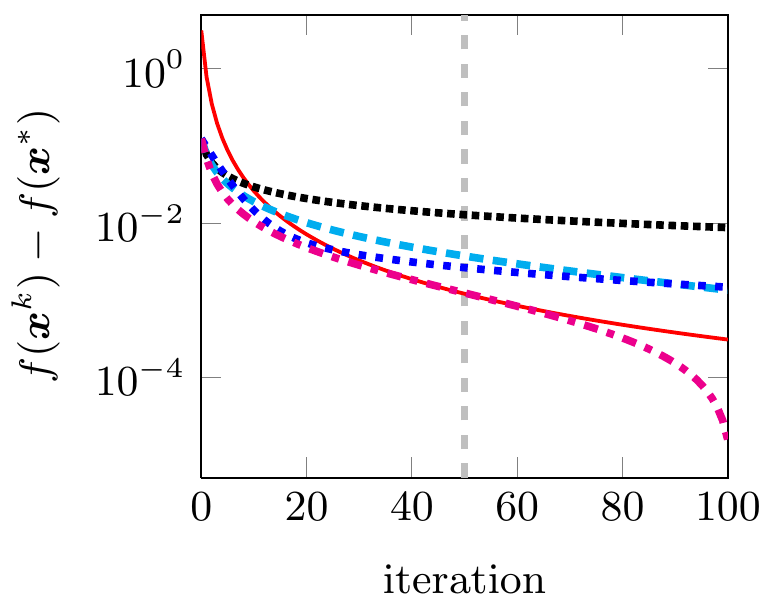
We extended the applicability of the Heavy-ball method from smooth unconstrained optimization to a class of non-smooth non-convex optimization problems: problems that are the sum of a continuously differentiable function with Lipschitz continuous gradient and a non-smooth non-convex extended-valued function with a simple proximal mapping. The algorithm was termed iPiano. We proved global subsequential convergence of the algorithm to a stationary point. Moreover, this is the first work that proves global convergence of an inertial algorithm for non-smooth non-convex optimization problems. This global convergence result is holds for objective functions that satisfy the so-called Kurdyka--Lojasiewicz inequality. This is a mild assumption that is satisfied by most of the functions in practical applications. iPiano has shown state-of-the-art performance for several problems from image processing.

P. Ochs:
Unifying abstract inexact convergence theorems and block coordinate variable metric iPiano.

SIAM Journal on Optimization, 29(1):541-570, 2019.

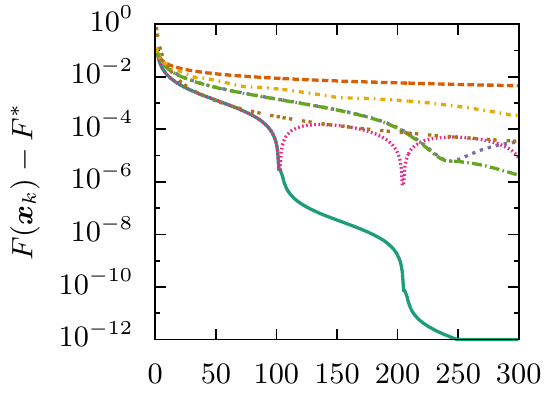
The contribution of this work is twofold: The first one is a unification of abstract convergence theorems for Kurdyka--Lojasiewicz functions. The second one uses the abstract convergence results to derive a block coordinate and variable metric variant of iPiano.

P. Ochs:
Local Convergence of the Heavy-ball Method and iPiano for Non-convex Optimization.

Journal of Optimization Theory and Applications, 177(1):153-180, 2018.

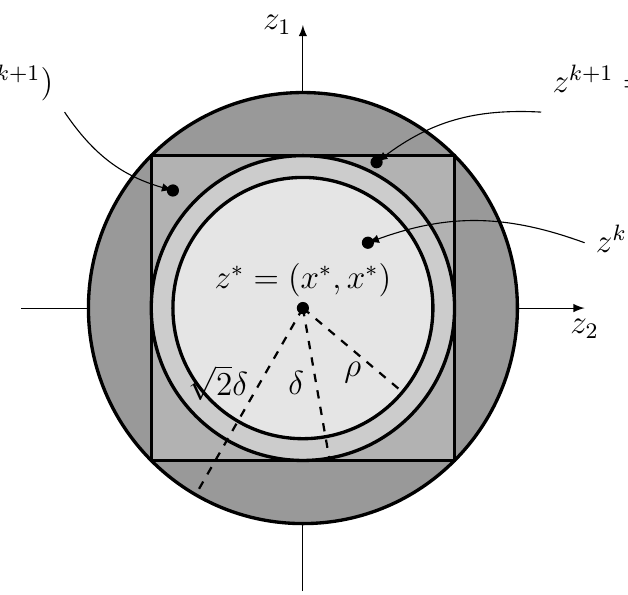
We studied the local convergence of iPiano for a class of so-called prox-regular functions. The local convergence result shows an equivalence of iPiano to inertial alternating/averaged proximal minimization/projection methods and therefore allowed us to tranfer the convergence results to these algorithms. Key is a formula for prox-regular functions that expresses the gradient of the Moreau envelope using the proximal mapping, which is well known in the convex setting.

M.C. Mukkamala, P. Ochs, T. Pock, S. Sabach:
Convex-Concave Backtracking for Inertial Bregman Proximal Gradient Algorithms in Non-Convex Optimization.

SIAM Journal on Mathematics of Data Science, 2(3):658-682, 2020.

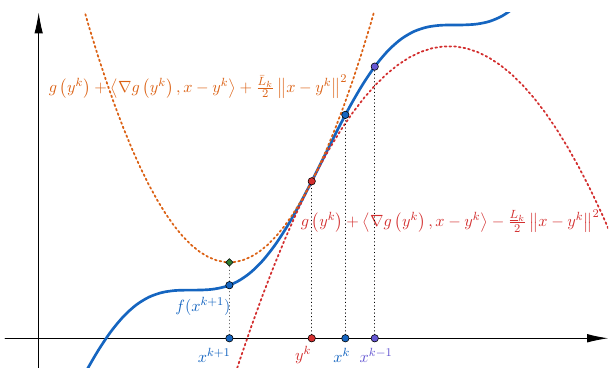
The inertial algorithm with Nesterov-like extrapolation and Bregman distances proposed in this work is significant due to several reasons: (i) We introduce a novel convex concave inertial (CoCaIn) backtracking strategy. Key is the observation that the use of inertia is closely connected to certain lower bound estimates of the objective function---non-inertial methods only rely on certain simple upper bounds. Intuitively, the algorithm adapts to the "local convexity" of the objective via an efficient backtracking strategy. (ii) The algorithm shows state-of-the-art performance on several problems from Machine Learning and Computer Vision. (iii) We present the first global convergence result for an inertial algorithm with Bregman distances to a stationary point for Kurdyka--Lojasiewicz functions.

P. Ochs, T. Pock:
Adaptive Fista for Non-convex Optimization.

SIAM Journal on Optimization, 29(4):2482-2503, 2019.

This work establishes a close connection between inertial algorithms and quasi-Newton methods. In particular, using a certain optimized extrapolation step, the SR1 quasi-Newton method can be recovered. Thanks to recent results on proximal calculus with respect to a rank-1 modified metric [BF12] S. Becker and J. Fadili: A Quasi-Newton Proximal Splitting Method. In Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS), 2618--2626, 2012. and the extension to proximal calculus for a rank-r modified metric, the resulting update step in Adaptive FISTA can be computed efficiently also for non-smooth non-convex additive composite problems.

The following works contribute to inertial algorithms in the convex setting.

P. Ochs, T. Brox, T. Pock:
iPiasco: Inertial Proximal Algorithm for strongly convex Optimization.

Journal of Mathematical Imaging and Vision, 53(2):171-181, 2015.

D. Hafner, P. Ochs, J. Weickert, M. Reißel, S. Grewenig:
FSI schemes: Fast semi-iterative solvers for PDEs and Optimisation Methods.

In B. Andres, B. Rosenhahn (Eds.): German Conference on Pattern Recognition (GCPR). Lecture Notes in Computer Science, Vol. 9796, 91-102, Springer, 2016. (Best Paper Award)

J.A. Tomasson, P. Ochs, J. Weickert:
AFSI: Adaptive restart for fast semi-iterative schemes for convex optimisation.

In T. Brox, A. Bruhn, M. Fritz (Eds.): German Conference on Pattern Recognition (GCPR). Lecture Notes in Computer Science, Vol. 11269, 669-681, Springer, 2019.