Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Convex Analysis and Optimization

Lecturer: Peter Ochs

Summer Term 2024
Lecture (4h) and Tutorial (2h)
9 ECTS

Lecture: Tuesday 12-14 c.t. in HS003, E1.3
Lecture: Thursday 10-12 c.t. in HS003, E1.3
Date of First Lecture: Tuesday, 16. April, 2024

Teaching Assistant: Shida Wang

Tutorials: by arrangement.
Core Lecture for Mathematics and Computer Science
Language: English
Prerequisites: Basics of Mathematics
(e.g. Linear Algebra 1-2, Analysis 1-3, Mathematics 1-3 for Computer Science)

News	Description	Registration
Exam	Schedule	Literature

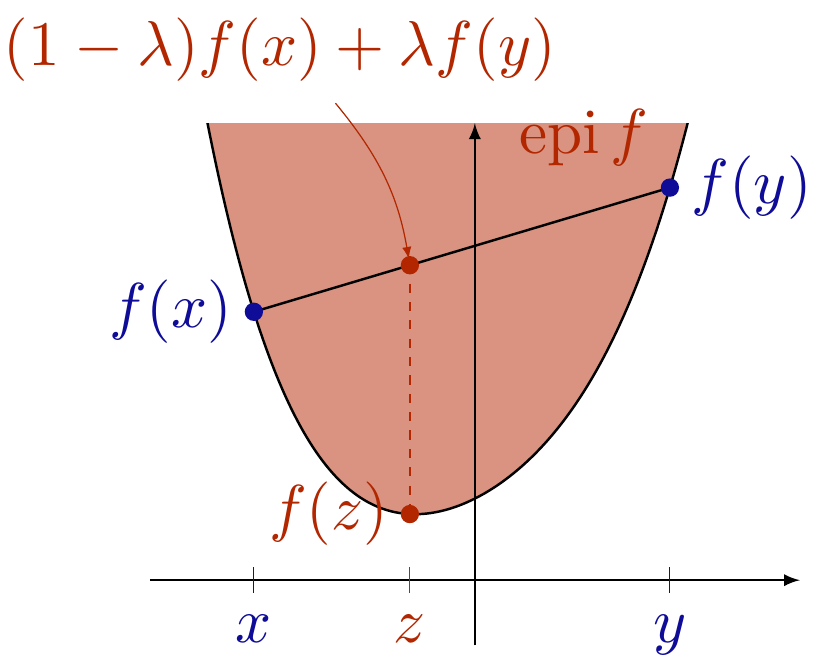
News

07.03.2024: Webpage is online.

Description

T. Rockafellar stated in a SIAM review: "The watershed in optimization is between convexity and non-convexity instead of linearity and non-linearity". For many decades linear optimization problems were considered as solvable and non-linear problems as very difficult to solve. However, the development of fundamental convex analysis tools such as Fenchel duality changed this picture. A broad and deep understanding of the theory led to many efficient algorithms for convex optimization problems, which has also contributed to the advance of applications, for example, in machine learning, computer vision, image processing, and compressed sensing.

The course introduces basic and advanced concepts of convex analysis. After definition, generation, and relations of convexity for sets and functions are studied, slightly more advanced tools such as the Moreau envelope, the subdifferential, and Fermat's rule are developed. These tools are fundamental for the study of convex optimization problems, optimality conditions, and algorithms. The second part of the lecture is devoted to the analysis of first order convex optimization algorithms that are ubiquitious in data science applications such as Image Processing, Computer Vision, Machine Learning and Statistics. Then, the study of convex duality allows us to introduce widely used primal-dual algorithms.

After taking the course, students know about the most relevant concepts of convex analysis and convex optimization. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of convex optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they develop basic skills in solving practical problems with Python.

Registration:

The coure will be organized via Moodle.

Exam:

Oral or written exam depending on the number of students.

Documentation and Schedule:

Participants of this lecture may download the course material directly from Moodle, including detailed lecture notes (script) and exercise sheets. Please note that the documentation that is provided is not meant to replace the attendance of the lectures and tutorials, that it may contain errors, and that it is not exclusively meant to define the contents of the exam.

The table of contents of the lecture is as follows:

Introduction

Introduction
Applications

Convex Geometry

Foundations
Convex Feasibility Problems

Convex Analysis Background

Preliminaries
Convex Functions

Smooth Convex Optimization

Optimality Conditions
Gradient Descent Method
Lower complexity bounds
Accelerated and Inertial Algorithms

Non-smooth Convex Analysis

Continuity of Convex Functions
Convexity from Epigraphical Operations
The Subdifferential

Non-smooth Convex Optimization

Fermat’s Rule
Duality in Optimization and Primal / Dual Problems
Algorithms
Lower complexity bounds
Saddle Point Problems

Literature

The lecture is based on the following literature, which is available via the library.

T. Rockafellar: Convex Analysis. Princeton University Press, 1970.
Y. Nesterov: Introductory Lectures on Convex Optimization - A Basic Course. Kluwer Academic Publishers, 2004.
D. P. Bertsekas: Convex Analysis and Optimization. Athena Scientific, 2003.
S. Boyd: Convex Optimization. Cambridge Univeristy Press, 2004.
H. H. Bauschke and P. L. Combettes: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, 2011.
T. Rockafellar and R. J.-B. Wets: Variational Analysis. Springer-Verlag Berlin Heidelberg, 1998.