Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Machine Learning

Lecturer: Peter Ochs

Summer Term 2025
Lecture (4h) and Tutorial (2h)
9 ECTS

Lecture: Monday 14-16 c.t. in Günter-Hotz, E2.2.
Lecture: Thursday 12-14 c.t. in Günter-Hotz, E2.2.
Date of First Lecture: Tuesday, 10. April, 2025

Teaching Assistant: Armin Beck

Core Lecture for Mathematics and Computer Science
Language: English
Prerequisites: Basics of Mathematics
(e.g. Linear Algebra 1-2, Analysis 1-3, Mathematics 1-3 for Computer Science)

Description

Registration

Literature

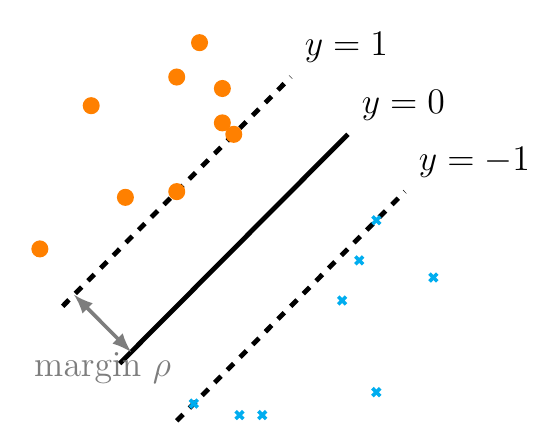
18.03.2025: Webpage is online.

Description

In this course we will introduce the foundations of machine learning (ML). In particular, we will focus on understanding the theoretical aspects of ML that have made ML successful in a wide range of applications such as bioinformatics, computer vision, information retrieval, computer linguistics, robotics, etc.

The course gives a broad introduction into machine learning methods from a theoretical point of view. After the lecture the students should be able to solve and analyze learning problems.

The tentative list of topics covers:

Probability theory
Maximum Likelihood/Maximum A Posteriori Estimators
Bayesian decision theory
Linear classification and regression
Model selection and evaluation
Convex Optimization
Kernel methods
Societal Impact of Machine Learning
Unsupervised learning (Clustering, Dimensionality Reduction)
Introduction to Deep Learning

Registration:

The coure will be organized via CMS.

Literature

The lecture is based on the following literature.

Bach, F.: Learning Theory from First Principles. Lecture Notes, available online, 2024.
Bishop, C. M.: Pattern recognition and machine learning. Springer, 2006
Duda, R. O., Hart, P.E., and Stork, D.G.: Pattern classification (2nd edition). Wiley-Interscience 2000
Boyd, S. P., and Vandenberghe, L.: ;Convex optimization. Cambridge university press, 2004
Hastie, T., Tibshirani, R., and Friedman, J.: The Elements of Statistical Learning. Springer, 2009.

Smola, A. J., : &ichölkopf, B.: Learning with kernels. GMD-Forschungszentrum Informationstechnik, 1998.

Goodfellow, I., Courville, A., and Bengio, Y.: Deep learning. MIT press, 2016.

Simon J.D. Prince: Understanding Deep Learning, MIT press, 2023.