Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Seminar on Machine Learning for Optimization
(Learning to Optimize)

Lecturer: Peter Ochs

Summer Term 2024
Seminar for Mathematics and Computer Science
7 ECTS

Time: Tuesday 2 - 4 pm.
First meeting: 23.04.2023

Teaching Assistants: Camille Castera and Sheheryar Mehmood

Language: English
Prerequisites: Basics of Mathematics
(e.g. Linear Algebra 1-2, Analysis 1-3, Mathematics 1-3 for Computer Science)
Basic understanding of Optimization
Basics of Machine Learning are recommended but not required.

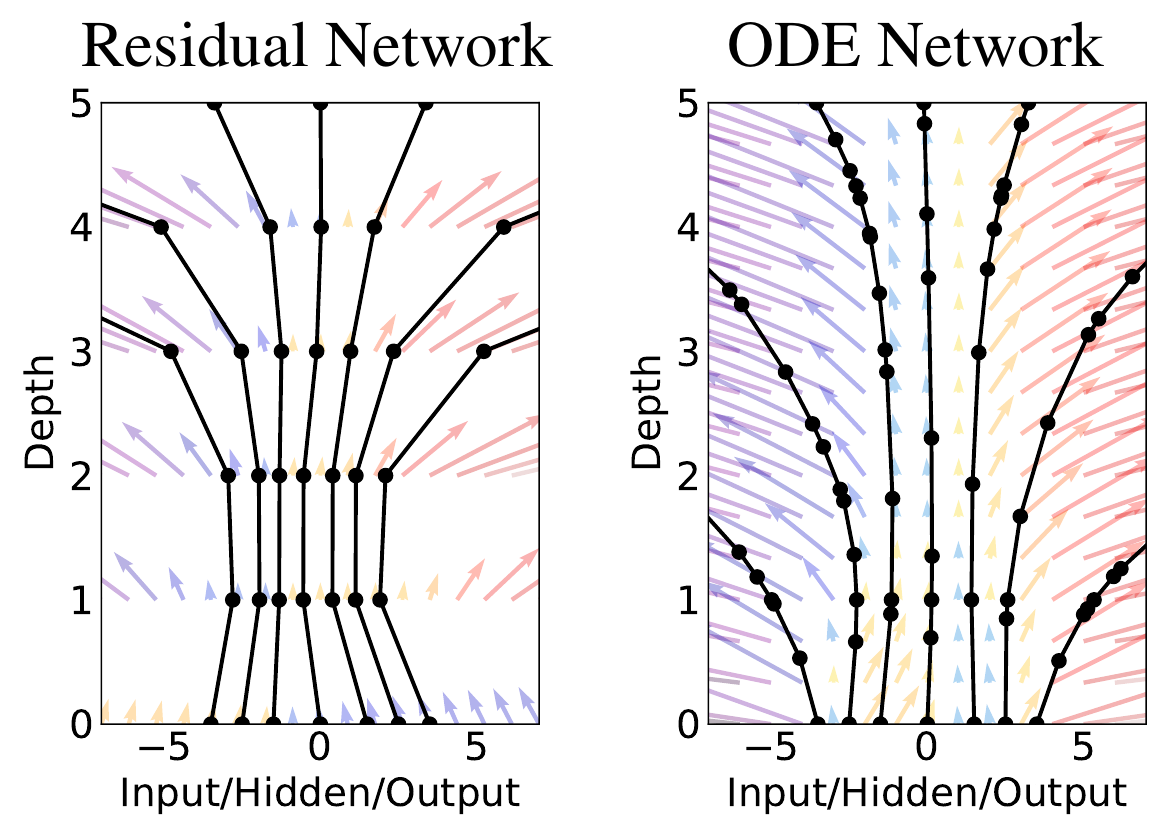[Chen et al. 2018]

News	Description	Registration
Grading	Schedule

News

08.04.2024: Table of references uploaded.
11.03.2024: Webpage is online.

Description

The recently growing field of Learning to optimize (L2O) leverages machine learning techniques to develop optimization methods and shares close relations to Meta-Learning. While classic optimization algorithms are hand crafted and proved to work for certain classes of problems, L2O automates the design based on a (training) data set of typical problems. L2O approaches are data-driven and are therefore tailored to a specific distribution of problems. On one hand, this is achieved by exploiting statistical features and unlocks solution strategies that outperform classical optimization algorithms by several orders of magnitude, however, on the other hand, usually there is no or little theoretical guarantees on the actual performance for a new problem. Generalization bounds like in Empirical Risk Minimization of Statistical Learning in general can be employed to provide some evidenve for in-distribution problems. However, typically such an approach is prone to fail for out-of-distribution problems. Therefore, the worlds of L2O and classical optimization must be brought closer together to achieve reliability and speed at the same time. In this seminar, we explore some important research attempts in the world of L2O.

Registration:

Register via the Seminar Assignment System at SIC Seminars.

For students from mathematics who cannnot register via this system, please write an eMail to Peter Ochs.

Requirements for Successful Participation:

Format: (in-person participation only)

Each student is assigned to three papers (assigned by us): one student gives the presentation on the paper, and the two other students take the role of moderators, i.e., they lead the discussion after the presentation.

Rules:

Presenter: Talk duration is 50 min (20 min on preliminaries + 30 minutes on the paper), plus 25 min for discussion. You may give a presentation using a projector and/or white/blackboard, optionally include experiments but not an obligation.
Moderator: Prepare meaningful questions and lead the discussion.
No Written summary is expected.
Regular attendance: You must attend all seminar meetings, except for provable important reasons (medical certificate).
Plagiarism: Adhere to the standards of scientific referencing and avoid plagiarism: Quotations and copied material (such as images) must be clearly marked as such, and a bibliography is required. Otherwise the seminar counts as failed.
Mandatory consultation: Talk preparation has to be presented to your seminar supervisor no later than one week before the talk is given. It is your responsibility to approach the supervisor timely and make your appointment.
Participation in discussions: The discussions after the presentations are a vital part of this seminar. This means that the audience (i.e. all participants) poses questions and tries to find positive and negative aspects of the proposed idea. This participation is part of your final grade.
Being in time: To avoid disturbing or interrupting the speaker, all participants have to be in the seminar room in time. Participants who turn out to be regularly late must expect a negative influence on their grade.

Documentation and Schedule:

References	Date
INTRO: organization, how to give good presentations, basics of optim, deep learning and training	23.04.2024
Andrychowicz, Denil, Gomez, Hoffman, Pfau, Schaul, Shillingford, de Freitas: Learning to learn by gradient descent by gradient descent, 2016.
Metz, Freeman, Harrison, Maheswaranathan, Sohl-Dickstein: Practical tradeoffs between memory, compute, and performance in learned optimizers, 2022.
Li, Malick: Learning to Optimize, 2016.
Venkatakrishnan, Bouman, Wohlberg: Plug-and-Play priors for model based reconstruction, 2013.
Meinhardt, Moeller, Hazirbas, Cremers: Learning Proximal Operators: Using Denoising Networks for Regularizing Inverse Imaging Problems, 2017.
Gregor, LeCun: Learning Fast Approximations of Sparse Coding, 2010.
Ablin, Moreau, Massias, Gramfort: Learning step sizes for unfolded sparse coding, 2019.
Long, Lu, Ma, Dong: PDE-Net: Learning PDEs from Data, 2017.
Heaton, Chen, Wang, Yin: Safeguarded Learned Convex Optimization, 2020.
Moeller, Möllenhoff, Cremers: Controlling Neural Networks via Energy Dissipation, 2019.
Wang, Yuan, Wu, Ge: Guarantees for Tuning the Step Size using a Learning-to-Learn Approach, 2020.
Chen, Rubanova, Bettencourt, Duvenaud: Neural Ordinary Differential Equations, 2018.
Graikos, Malkin, Jojic, Samaras: Diffusion models as plug-and-play priors, 2022.