Mathematical Optimization for Data Science Group, Saarland University

Welcome to the homepage of the

Mathematical Optimization for Data Science Group

Department of Mathematics and Computer Science, Saarland University, Germany

Dynamical System View on Optimization

Optimization algorithms can be seen as discretized versions of solutions of ordinary differential equations (ODEs). These solutions of ODEs often exhibit similar properties as their algorithmic counterparts while being easier to analyze. Their analyses also provide roadmaps for proving similar results for optimization algorithms. Our research makes use of this strong connection between dynamical systems and optimization algorithms to provide new insights into existing methods, but also to design new ones backed by strong theoretical justification.

Partially funded by the German Research Foundation (DFG Grant OC 150/5-1).

Our Contribution:

[CAFO24] C. Castera, H. Attouch, J. Fadili, P. Ochs:
Continuous Newton-like Methods featuring Inertia and Variable Mass.

SIAM Journal on Optimization, 34(1):251-277, 2024.

In the last decade, many algorithms were derived from the Dynamical Inertial Newton-like (DIN) family of ODEs first introduced by [AABR02]. This is a family of ODEs mixing inertial gradient descent and Newton's method, positioning them at the interface of first- and second-order optimization. Unfortunately, most of them seem to be closer to first-order methods than second-order ones. We introduce a new system called VM-DIN-AVD, featuring two non-constant parameters called variable mass and damping. The system encompasses the main first- and second-order ODEs encountered in optimization, via speficic choices of the two parameters. The main result shows that the variable mass parameter allows making VM-DIN-AVD arbitrarily close to Newton's method, ensuring that the system is of second-order nature.

[MCO23] S. Maier, C. Castera, P. Ochs:
Near-optimal Closed-loop Method via Lyapunov Damping for Convex Optimization.

Technical Report, ArXiv e-prints, arXiv:2311.10053, 2023.

The optimal algorithm for first-order convex optimization proposed by [Nesterov83] can also be understood through the lens of ODEs. [SBC15] proposed an ODE to model this method (which is a special case of VM-DIN-AVD introduced in [CAFO24] above). This ODE is said to be non-autonomous because it features a "damping" that directly involves the time variable. The drawback of this is that the choice of the initial time (which is arbitrary) influences the ODE. A difficult open problem consists in replacing this damping by one that does not depend directly on the time, while preserving the optimal speed of convergence, which is hard since the optimality of the method comes exactly from this damping. We propose a new technique called Lyapunov damping that fixes the aforementioned issue and for which we prove a rate of convergence arbitrarily close to the optimal one.

[NCFO23] T. Natu, C. Castera, J. Fadili, P. Ochs:
Accelerated Gradient Dynamics on Riemannian Manifolds: Faster Rate and Trajectory Convergence.

Technical Report, ArXiv e-prints, arXiv:2312.06366, 2023.

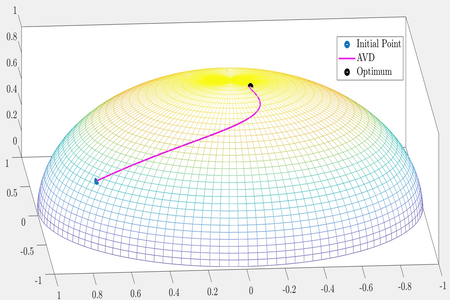
To optimize a real valued differentiable convex function defined on a Riemannian manifold, we study accelerated gradient dynamics with an asymptotically vanishing damping term. In this work, we close the gaps between the convergence guarantees for accelerated gradient dynamics in the Euclidean setting and the Riemannian setting. In particular, when the damping parameter is strictly greater than a certain curvature-dependent constant, we improve the convergence rate of objective values than the previously known rate. In the same setting, we prove the convergence of trajectory of the dynamical system to an element in the set of minimizers of the objective function. When the damping parameter is smaller than this curvature-dependent constant, the best known sub-optimal rates for the objective values and the trajectory are transferred to the Riemannian setting. We present computational experiments that confirm our theoretical results.

[MFA22] R. Maulen-Soto, J. Fadili, H. Attouch:
An SDE perspective on stochastic convex optimization.

Technical Report, ArXiv e-prints, arXiv:2207.02750, 2022.

We analyze the global and local behavior of gradient-like flows under stochastic errors towards the aim of solving convex optimization problems with noisy gradient input. We first study the unconstrained differentiable convex case, using a stochastic differential equation where the drift term is minus the gradient of the objective function and the diffusion term is either bounded or square-integrable. In this context, under Lipschitz continuity of the gradient, our first main result shows almost sure weak convergence of the trajectory process towards a minimizer of the objective function. We also provide a comprehensive complexity analysis by establishing several new pointwise and ergodic convergence rates in expectation for the convex, strongly convex, and (local) Lojasiewicz case. The latter, which involves local analysis, is challenging and requires non-trivial arguments from measure theory. Then, we extend our study to the constrained case and more generally to certain nonsmooth situations. We show that several of our results have natural extensions obtained by replacing the gradient of the objective function by a cocoercive monotone operator.

[MFA24] R. Maulen-Soto, J. Fadili, H. Attouch:
Tikhonov Regularization for Stochastic Non-Smooth Convex Optimization in Hilbert Spaces.

Technical Report, ArXiv e-prints, arXiv:2403.06708, 2024.

To solve convex optimization problems with a noisy gradient input, we analyze the global behavior of subgradient-like flows under stochastic errors. The objective function is composite, being equal to the sum of two convex functions, one being differentiable and the other potentially non-smooth. We then use stochastic differential inclusions where the drift term is minus the subgradient of the objective function, and the diffusion term is either bounded or square-integrable. In this context, under Lipschitz's continuity of the differentiable term and a growth condition of the non-smooth term, our first main result shows almost sure weak convergence of the trajectory process towards a minimizer of the objective function. Then, using Tikhonov regularization with a properly tuned vanishing parameter, we can obtain almost sure strong convergence of the trajectory towards the minimum norm solution. We find an explicit tuning of this parameter when our objective function satisfies a local error-bound inequality. We also provide a comprehensive complexity analysis by establishing several new pointwise and ergodic convergence rates in expectation for the convex and strongly convex case.

[MFAO24] R. Maulen-Soto, J. Fadili, H. Attouch, P. Ochs:
Stochastic Inertial Dynamics Via Time Scaling and Averaging.

Technical Report, ArXiv e-prints, arXiv:2403.16775, 2024.

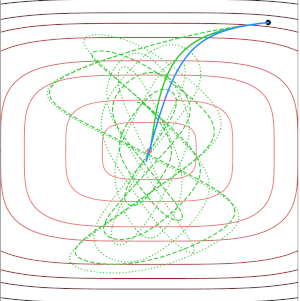
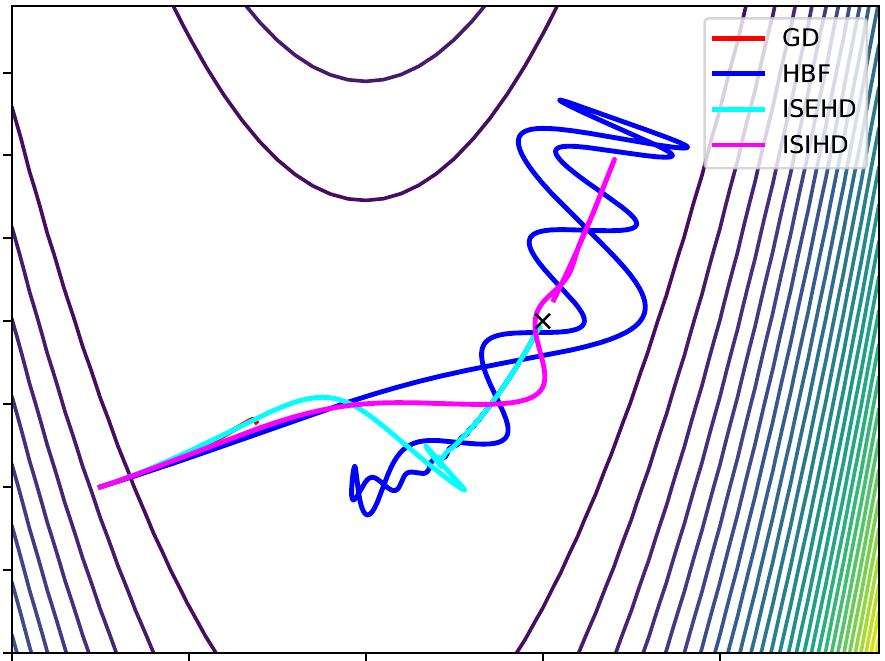
As pointed out in [MCO23], the Nesterov algorithm can be seen through the lens of ODEs (see [SBC15], the resulting algorithm has a so-called ''viscous damping''. In practice, one of the drawbacks of the resulting ODE denoted ''AVD'' is the oscillations of the trajectory (and of the values) towards the minima for ill-conditioned problems. To overcome this, the introduction of a geometric Hessian Damping was first considered by [ALP21], then analised in depth in [ACFR23] and [AFK23]. This can be done in an explicit or implicit manner, resulting in the second-order (in time) systems called ISEHD or ISIHD, respectively. Moreover, in [ABN23] they show that, in the convex setting, if we apply a time rescaling and averaging to Gradient Flow, we end up with an instance of ISIHD, being able to transfer the known results of Gradient Flow to this second-order (in time) dynamic. Our idea in this paper is to make use of that result and extend it to the stochastic and non-smooth setting, i.e., apply a time rescaling and averaging to the SDI studied in [MFA24], which can be seen as the stochastic version of the differential inclusion studied by [Brezis83] to end up with an instance of the stochastic non-smooth version of ISIHD, making the analysis much simpler after the transfer of the already established results for the SDI. In this case, we obtain fast convergence results for the viscous damping of and a properly tuned implicit Hessian Damping, under mild integrability conditions on the noise.