Welcome to the homepage of the
Mathematical Optimization for Data Science Group
Department of Mathematics and Computer Science, Saarland University, Germany
|
Learning to Optimize |
| Typically, optimization algorithms are derived analytically by considering a certain class of problems for which one can perform a worst-case analysis to prove convergence and derive corresponding convergence rates. This approach provides a theoretically guaranteed performance of the algorithm for any case in question. However, this comes at a cost: The worst-case analysis often forbids to use statistical properties of the problem, and the analytical tractability severly limits the design choices. As a result, many classical optimization algorithms are robust and easy to implement, yet their actual performance might prove to be unsatisfactory in many cases. On the other hand, the recently growing field of Learning-to-Optimize leverages machine learning techniques to develop optimization methods. Especially, this alleviates the bounds of analytical tractability and allows for automation of their design in a data-driven manner. As a result, learned algorithms are often able to outperform classical ones by several order of magnitude by utilizing more of the statistical properties that prevail in the given distribution of problems. However, also this comes at a cost: By explicitly going beyond analtic features, one looses the typical convergence guarantees for the learned algorithm, which would render its application at least questionable. | ||||||||
|
| ||||||||
|
One way to mitigate this problem is by means of generalization results: Since the algorithm is actively trained on a given dataset, it typically solves the corresponding problems very efficiently. Thus, by proving that its performance generalizes to the whole data-generating distribution ("in-distribution generalization"), one gets an algorithm that is specifically tailored to these kind of problems and has a guaranteed performance on them.
Nevertheless, the learned algorithm still might fail on problems stemming from different distributions ("out-of-distribution generalization"), that is, it might not be applicable to whole classes of problems without any further ado.
Therefore, the worlds of Learning-to-Optimize and classical optimization have to be brought closer together to achieve reliability and speed at the same time.
| ||||||||
| Our Contributions: | ||||||||
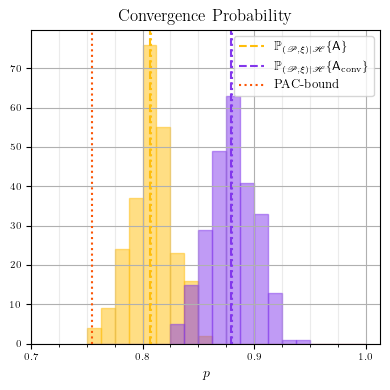
We present a theoretical framework for learning optimization algorithms based on the empirical risk. In this framework, we measure the performance of the algorithm by means of the loss of the last iterate, and the algorithm is assumed to be parametric, that is, it has hyperparameters that have to be chosen by the user to optimize its performance. In doing so, we provide PAC-Bayesian generalization guarantees, that is, we are able to learn a distribution over these hyperparameters in a data-driven way, which guarantees that, with high-probability, the performance of the algorithm on the training data generalizes to the whole data-generating distribution (that defines the class of optimization problems).
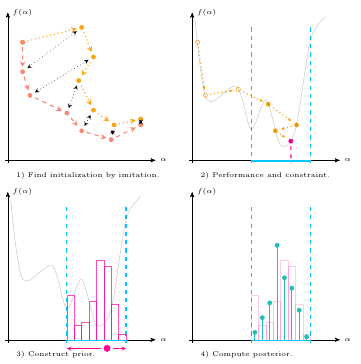
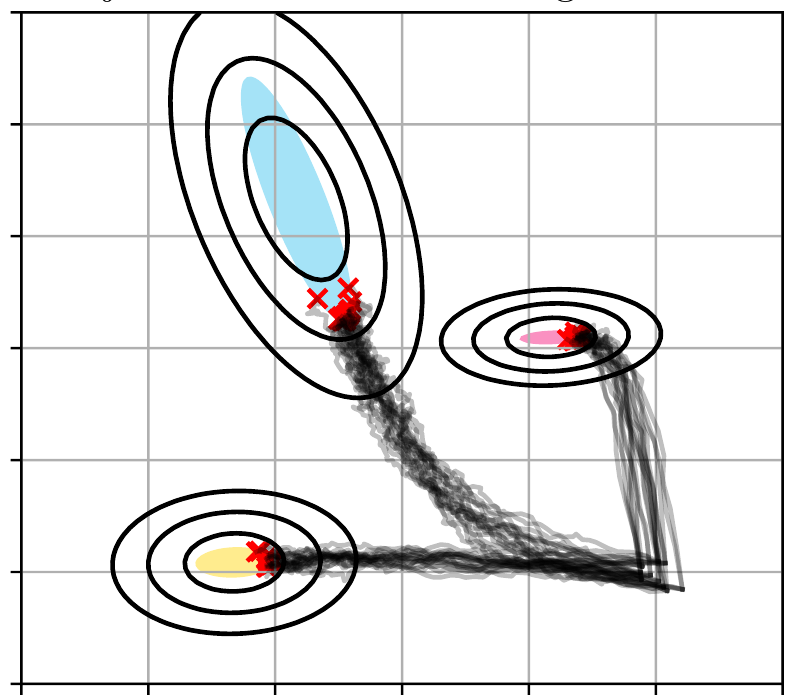
The PAC-Bayesian approach to learning has received considerable attention in recent years. Typically, this approach is built upon a so-called prior distribution, and it was reported many times that the achieved performance and the given guarantees rely heavily on the actual choice of this distribution. We also discovered this problem in our conference paper [SO23] and subsequent experiments. However, based on our theoretical constraints, we actively have to construct a suitable distribution. In doing so, we report several (new and crucial) design choices for Learning-to-Optimize, for example, a very specific loss-function for training. To validate the procedure and our theoretical generalization guarantees, we conduct four experiments, ranging from strongly convex and smooth problems up to non-smooth and non-convex problems. Taken together, we present a complete framework for learning optimization algorithms with PAC-Bayesian guarantees.
We present a probabilistic model for stochastic iterative algorithms with the use case of optimization algorithms in mind. Based on this model, we present PAC-Bayesian generalization bounds for functions that are defined on the trajectory of the learned algorithm, for example, the expected (non-asymptotic) convergence rate and the expected time to reach the stopping criterion. Thus, not only does this model allow for learning stochastic algorithms based on their empirical performance, it also yields results about their actual convergence rate and their actual convergence time. We stress that, since the model is valid in a more general setting than learning-to-optimize, it is of interest for other fields of application, too. Finally, we conduct five practically relevant experiments, showing the validity of our claims.
Conventional convergence guarantees in optimization are based on geometric arguments, which cannot be applied easily to learned algorithms. Therefore, in this work we present a probabilistic framework that resembles deterministic optimization and allows for transferring geometric arguments into learning-to-optimize. In doing so, we bring together advanced tools from optimization and learning theory: The main result is a generalization result for parametric classes of potentially non-smooth, non-convex loss functions, and allows to establish the convergence of learned optimization algorithms to stationary points with high probability. This can be seen as a statistical counterpart to the use of geometric safeguards to ensure convergence. | ||||||||
Towards designing learned optimization algorithms that are usable beyond their training setting (the aforementioned out-of-distribution case), we identify key principles that classical algorithms obey, but have up to now, not been used for Learning to Optimize (L2O). Following these principles, we provide a general design pipeline, taking into account data, architecture and learning strategy, and thereby enabling a synergy between classical optimization and L2O, resulting in a philosophy of Learning Optimization Algorithms. As a consequence our learned algorithms perform well far beyond problems from the training distribution. We demonstrate the success of these novel principles by designing a new learning-enhanced BFGS algorithm and provide numerical experiments evidencing its adaptation to many settings at test time. | ||||||||
In this work, we investigate how symmetries can be leveraged to obtain stronger PAC-Bayesian generalization guarantees. While symmetries are known to improve empirical performance, existing theory mostly covers compact groups and assumes that the data distribution itself is invariant, conditions rarely met in realistic learning-to-optimize settings. We extend PAC-Bayes guarantees to non-compact symmetries, such as translations, and to non-invariant data distributions, tightening existing bounds and demonstrating the approach using McAllester’s PAC-Bayes bound. Experiments on rotated MNIST with a non-uniform rotation group confirm that our guarantees hold in practice and improve upon prior results. Placed within the broader Learning-to-Optimize agenda, our results prepare the development of symmetry-aware learnable algorithms with provable generalization benefits. |
MOP Group
©2017-2025
The author is not
responsible for
the content of
external pages.
 Saarland
Saarland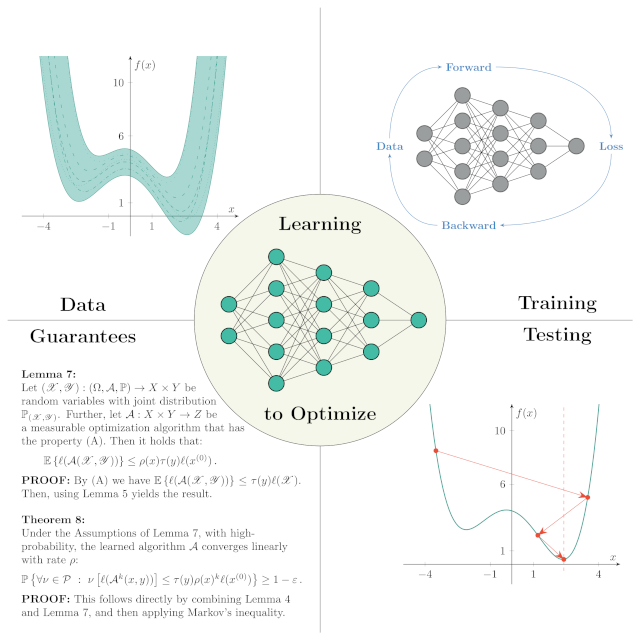

![[pdf]](/images/pdf_14x14.png)