Welcome to the homepage of the
Mathematical Optimization for Data Science Group
Department of Mathematics and Computer Science, Saarland University, Germany
|
TRINOM-DS: |
|
Structured composite non-smooth optimization has proved to be extremely useful in data science, where a common trend is the deluge of large-scale multidimensional data, which drives the need for more efficient optimization schemes. While, so far, primarily, first-order schemes have been widely used to solve such optimization problems, they are quickly approaching their natural (and provable) limitations. In contrast, higher-order methods, in particular quasi-Newton ones, are hardly used due to their lack of scalability, the complexity in their mathematical analysis and the deployment in the non-smooth case. TRINOM-DS will unlock these bottlenecks and develop theoretical, numerical and algorithmic advances to exploit the great potential of quasi-Newton-type schemes for non-smooth large-scale optimization problems, which are ubiquitous in data science. These algorithms will be developed in a variety of challenging settings and are expected to have far reaching applications in data science, e.g., machine learning (optimal transport, deep learning, etc), imaging and computer vision. They will be implemented as fast optimization codes, possibly on dedicated architectures, that will be made publicly available following the philosophy of reproducible research. TRINOM-DS's members are very active players in the European school of optimization and data science, which makes this project a unique opportunity to give a scalable, computational and practical embodiment to higher-order non-smooth optimization methods.
Funded by the ANR DFG 2020 NLE. | ||||||
| Our Contributions: | ||||||
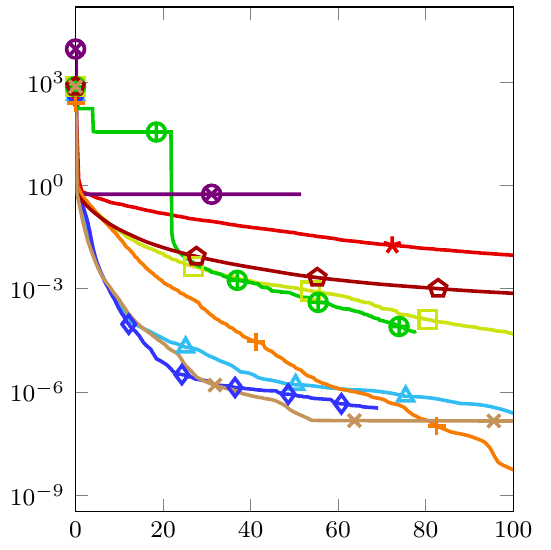
Quasi-Newton methods are widely used for optimization with sufficiently smooth objective functions. In order to solve a non-smooth composite problem efficiently, [BF12, BFO19] developed a proximal calculus for evaluating the proximal mapping w.r.t a variable metric generated from a quasi-Newton framework. In this paper, we extend their method to the evaluation of resolvent operators, based on which two inertial forward-backward quasi-Newton methods for monotone inclusions are designed. As a special example of monotone inclusion problems saddle point problems are considered and an efficient quasi-Newton Primal Dual Hybrid Gradient method is devised. | ||||||
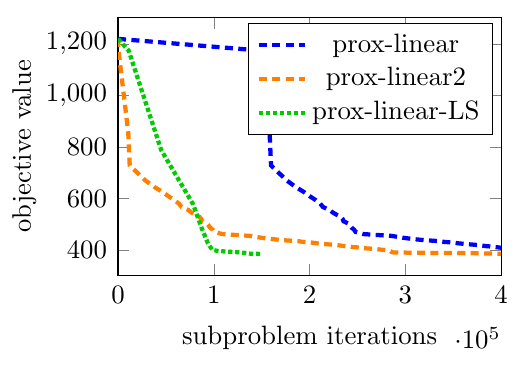
We design a quasi-Newton primal-dual algorithm that is tailored to a special class of saddle point problems, where we incorporate a limited-memory quasi-Newton metric with efficiently implementable proximal mapping. As compared to the general monotone inclusion setting in [WFO22], the specialization allows for an efficient line-search strategy and yields a primal-dual algorithm that outperforms the line-search based primal-dual algorithm (with identity metric) and the primal-dual algorithm from [WFO22] on a challenging image deblurring problem. | ||||||
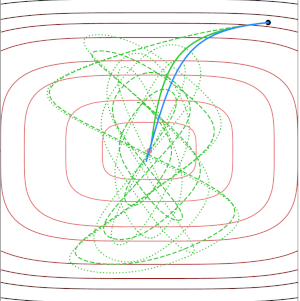
In the last decade, many algorithms were derived from the Dynamical Inertial Newton-like (DIN) family of ODEs first introduced by [AABR02]. This is a family of ODEs mixing inertial gradient descent and Newton's method, positioning them at the interface of first- and second-order optimization. Unfortunately, most of them seem to be closer to first-order methods than second-order ones. We introduce a new system called VM-DIN-AVD, featuring two non-constant parameters called variable mass and damping. The system encompasses the main first- and second-order ODEs encountered in optimization, via speficic choices of the two parameters. The main result shows that the variable mass parameter allows making VM-DIN-AVD arbitrarily close to Newton's method, ensuring that the system is of second-order nature. | ||||||
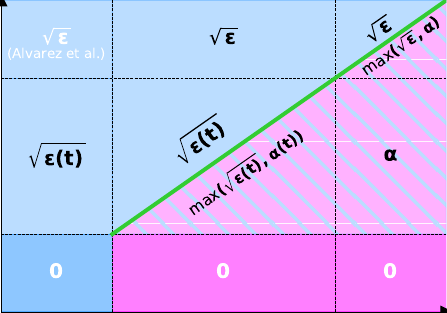
The optimal algorithm for first-order convex optimization proposed by [Nesterov83] can also be understood through the lens of ODEs. [SBC15] proposed an ODE to model this method (which is a special case of VM-DIN-AVD introduced in [CAFO24] above). This ODE is said to be non-autonomous because it features a "damping" that directly involves the time variable. The drawback of this is that the choice of the initial time (which is arbitrary) influences the ODE. A difficult open problem consists in replacing this damping by one that does not depend directly on the time, while preserving the optimal speed of convergence, which is hard since the optimality of the method comes exactly from this damping. We propose a new technique called Lyapunov damping that fixes the aforementioned issue and for which we prove a rate of convergence arbitrarily close to the optimal one. | ||||||
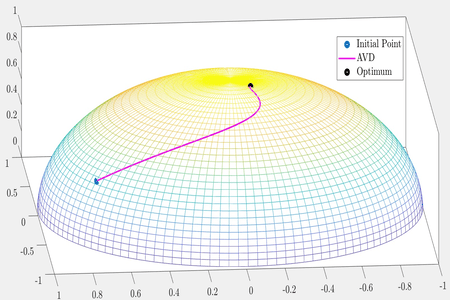
To optimize a real valued differentiable convex function defined on a Riemannian manifold, we study accelerated gradient dynamics with an asymptotically vanishing damping term. In this work, we close the gaps between the convergence guarantees for accelerated gradient dynamics in the Euclidean setting and the Riemannian setting. In particular, when the damping parameter is strictly greater than a certain curvature-dependent constant, we improve the convergence rate of objective values than the previously known rate. In the same setting, we prove the convergence of trajectory of the dynamical system to an element in the set of minimizers of the objective function. When the damping parameter is smaller than this curvature-dependent constant, the best known sub-optimal rates for the objective values and the trajectory are transferred to the Riemannian setting. We present computational experiments that confirm our theoretical results. | ||||||
We revisit the Ravine method of Gelfand and Tsetlin from a dynamical system perspective, study its convergence properties, and highlight its similarities and differences with the Nesterov accelerated gradient method. The two methods are closely related. They can be deduced from each other by reversing the order of the extrapolation and gradient operations in their definitions. They benefit from similar fast convergence of values and convergence of iterates for general convex objective functions. We will also establish the high resolution ODE of the Ravine and Nesterov methods and reveal an additional geometric damping term driven by the Hessian for both methods. This will allow us to prove fast convergence toward zero of the gradients not only for the Ravine method but also for the Nesterov method for the first time. In the strongly convex case, we show linear convergence for the Ravine method at an optimal rate. We also highlight connections to other algorithms resulting from more subtle discretization schemes and finally describe a Ravine version of the proximal-gradient algorithms for general structured smooth + nonsmooth convex optimization problems. | ||||||
We analyze the global and local behavior of gradient-like flows under stochastic errors towards the aim of solving convex optimization problems with noisy gradient input. We first study the unconstrained differentiable convex case, using a stochastic differential equation where the drift term is minus the gradient of the objective function and the diffusion term is either bounded or square-integrable. In this context, under Lipschitz continuity of the gradient, our first main result shows almost sure weak convergence of the trajectory process towards a minimizer of the objective function. We also provide a comprehensive complexity analysis by establishing several new pointwise and ergodic convergence rates in expectation for the convex, strongly convex, and (local) Lojasiewicz case. The latter, which involves local analysis, is challenging and requires non-trivial arguments from measure theory. Then, we extend our study to the constrained case and more generally to certain nonsmooth situations. We show that several of our results have natural extensions obtained by replacing the gradient of the objective function by a cocoercive monotone operator. | ||||||
To solve convex optimization problems with a noisy gradient input, we analyze the global behavior of subgradient-like flows under stochastic errors. The objective function is composite, being equal to the sum of two convex functions, one being differentiable and the other potentially non-smooth. We then use stochastic differential inclusions where the drift term is minus the subgradient of the objective function, and the diffusion term is either bounded or square-integrable. In this context, under Lipschitz's continuity of the differentiable term and a growth condition of the non-smooth term, our first main result shows almost sure weak convergence of the trajectory process towards a minimizer of the objective function. Then, using Tikhonov regularization with a properly tuned vanishing parameter, we can obtain almost sure strong convergence of the trajectory towards the minimum norm solution. We find an explicit tuning of this parameter when our objective function satisfies a local error-bound inequality. We also provide a comprehensive complexity analysis by establishing several new pointwise and ergodic convergence rates in expectation for the convex and strongly convex case. | ||||||
This work is part of the close link between continuous-time dissipative dynamical systems and optimization algorithms, and more precisely here, in the stochastic setting. We study stochastic convex minimization problems through the lens of stochastic inertial differential inclusions that are driven by the subgradient of a convex objective function. This provides a general mathematical framework for analyzing the convergence properties of stochastic second-order inertial continuous-time dynamics involving vanishing viscous damping and measurable stochastic subgradient selections. We develop a systematic and unified way that transfers the properties recently studied for first-order stochastic differential equations to second-order ones involving even subgradients in lieu of gradients. This program will rely on two tenets: time scaling and averaging, following an approach recently developed in the literature by one of the co-authors in the deterministic case. Under a mild integrability assumption involving the diffusion term and the viscous damping, our first main result shows that almost surely, there is weak convergence of the trajectory towards a minimizer of the objective function and fast convergence of the values and gradients. We also provide a comprehensive complexity analysis by establishing several new pointwise and ergodic convergence rates in expectation for the convex, strongly convex, and (local) Polyak-Lojasiewicz case. Finally, using Tikhonov regularization with a properly tuned vanishing parameter, we can obtain almost sure strong convergence of the trajectory towards the minimum norm solution. | ||||||
| Our Preliminary Work: | ||||||
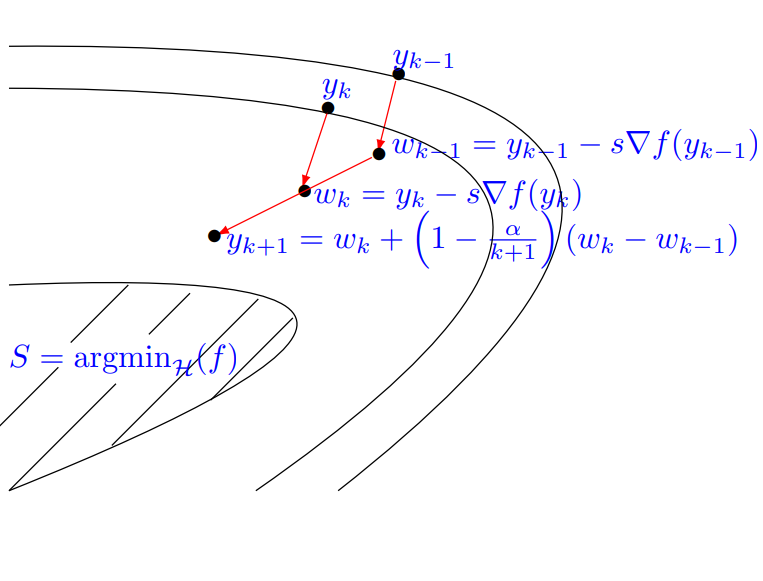
In our joint work on proximal quasi-Newton methods, we have built the basement for this project. The contribution distinguishes significantly from related work, which either study the theory of variable metric methods or their practical implementation. In contrast, we developed in [BF12] and [BFO19] an advanced and efficient proximal calculus for a common type of non-diagonal quasi-Newton metrics, which can be written as the sum of a diagonal matrix and a rank-r matrix. In particular, we have studied a proximal SR1- and BFGS-type quasi-Newton method with a favorable performance in practical convex optimization problems. While this contribution is a significant step towards the usage of quasi-Newton methods for non-smooth optimization, their establishment as generic state-of-the-art solvers for applications in large-scale data science requires successful completion of the work program in this project proposal. | ||||||
The surprising equivalence between types of (proximal) quasi-Newton methods and extrapolated (proximal) gradient based algorithms has been established. A certain choice of extrapolation leads exactly to the proximal SR1-metric used in [BF12] and [BFO19]. This equivalence yields a novel point of view on proximal quasi-Newton methods and serves as a basis for further development for both types of algorithms. | ||||||
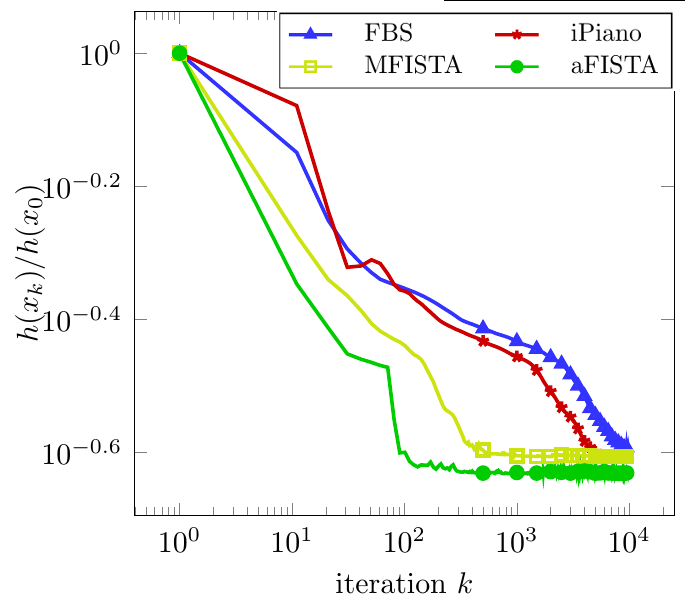
In [Ochs19] we developed a general and unifying view on convergence of descent methods for non-convex non-smooth optimization problems, which is inspired by [ABS13] H. Attouch, J. Bolte, and B. Svaiter: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Mathematical Programming, 137(1-2):91--129, 2013. . As a special case of the generalization, the framework allows convergence of inertial proximal gradient descent (iPiano) and its variable metric variant to be studied conveniently. In [OFB18], a unifying convergence framework for Bregman-based minimization algorithms was also developed. In [Ochs18], for a variant of the inertial methods just mentioned, we derived the local convergence (including convergence rates) and an equivalence to alternating minimization schemes. All this previous work provides a good theoretical basis for the convergence analysis of quasi-Newton methods in non-convex setting and the practical combination of quasi-Newton methods with extrapolation methods and/or Bregman distances. | ||||||
In [VPF15] and [LFP17], we have developed a unifying theory for exact low-complexity model finite-time identification by proximal splitting methods for a large class of regularizers called partly smooth functions. In [FMP18] and [FGMP18], a key limiting assumption of [VPF15], [LFP17] was removed, but for a smaller class of regularizers coined mirror-stratifiable functions, while ensuring finite-time approximate (but not exact) model identification. These results were the first to explain empirical observations made in inverse problems and machine learning. They will provide a good basis for the design and the analysis of scalable quasi-Newton methods when applied to solve problems with low-complexity regularization. |
MOP Group
©2017-2025
The author is not
responsible for
the content of
external pages.
 Saarland
Saarland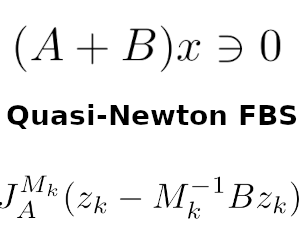
![[pdf]](/images/pdf_14x14.png)